• Lenta
• Tikslas
• Žaidimo eiga
• Komi

Alternatorius žaidžiamas ant 8x8 šaškių/šachmatų lentos:

Alternatoriaus tikslas yra turėti daugiau taškų nei priešininkas po to, kai abu žaidėjai praleidžia ėjimą.

Žaidėjo taškai yra jo spalvos medžių dydžių suma.

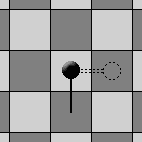
Pirmasis žaidėjas valdo juodus laukelius, o antrasis - baltus.

Žaidėjai eina paeiliui pradedant nuo žaidėjo valdančio juodus laukelius.

Ėjimas susideda iš dviejų dalių. Pirmiausiai nupiešiamas taškas laukelyje, kuriame dar nėra taško. Paskui nupiešiama tiesi linija iš to taško i šalimais esamo laukelio centrą, kuris dar neturi taško. Linija sujungia du gretimus priešingų spalvų laukelius. Laukelis, kuriame yra taškas, vadinamas "Duobe". Linija vadinama "Kamienu".  Laukelis, kuriame yra linijos galas, be taško, vadinamas "Šaknimi". "Duobė" ir "Kamienas" sudaro "Vyšnią"

Svarbi pastaba: žaidėjas, valdantas juodus laukelius, gali padeti "Vyšnią" su "Duobe" arba ant juodo laukelio arba ant balto. Tas pats galioja ir baltam žaidėjui.

A player drew a dot on a white cell and then drew a line from that dot to the lower black cell. The cell containing the dot is called "PIT". The lower black cell containing the other end of the line is called "ROOT".		A player cannot draw a dashed "CHERRY" because it's forbidden to draw a "ROOT" on the cell which already has a "PIT".

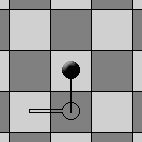
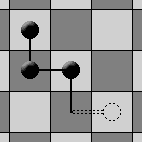
When you move, it is permitted to draw a new "PIT" on the "ROOT" of some "CHERRY" already on the board:

As the game proceeds, "CHERRIES" become connected to other "CHERRIES" by their "STEMS".  A connected group of cherries is called a "TREE".  For every "TREE" there is exactly one cell which is not a "PIT" but which forms the "ROOT" of at least one "CHERRY" in that "TREE".  This cell is called the "TREE’S ROOT".  Note that a single "CHERRY" is just a special case of a "TREE".

The player who owns the cell which forms the "ROOT" of a "TREE" owns that entire "TREE".  However, the addition of a new "CHERRY" may result in the other player owning that "TREE".  The owner of each "TREE" is ascertained only after the game has ended.

The "SIZE" of a "TREE" is the number of cells which it occupies, including its "ROOT".  A "TREE's SIZE" is always one more than the number of "PITS" in that "TREE" (a single "CHERRY" is a "TREE" of size 2).  A tree contributes a number of points equal to its "SIZE" to the player who owns that "TREE".  Note: An empty cell which is not the "ROOT" or "PIT" of any "CHERRY" contributes one point to the owner of that cell.  It is a "TREE" of size 1.

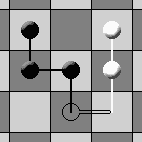
It is possible to merge two separate "TREES" whose "ROOTS" occupy adjacent squares.  This is accomplished by placing the "PIT" of a new "CHERRY" over the "ROOT" of one of these "TREES" and the "ROOT" of that "CHERRY" in the cell containing the "ROOT" of the other "TREE":

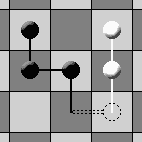
If two "TREES" can merge, but one has larger size than the other, then the larger "TREE" must be attached to the smaller "TREE".

In other words the "CHERRY" which merges "TREES"  must have its "PIT" on the "ROOT" of the larger "TREE" and its "ROOT" on the "ROOT" of the smaller "TREE".

The "ROOT" of the resulting "TREE" will be on the cell which contained the "ROOT" of the smaller of the two original "TREES".

When two "TREES" of equal size merge, it does not matter which "ROOT" becomes the "ROOT" of the resulting "TREE".

A player can merge black and white "TREES" by drawing a "CHERRY" with its "PIT" on the "ROOT" of the larger "TREE" (the black one) and its "ROOT" on the "ROOT" of the smaller "TREE" (the white one).	A player cannot attach the white "TREE" to the black "TREE" because the black tree is larger and it's forbidden to attach smaller "TREE" to the larger one.	A player cannot draw the specified "CHERRY" because it attaches a smaller "TREE" (the blank cell is a "TREE" of size 1) to the larger "TREE" (the size of the black tree is 4).

A player may always pass on his turn.  The game ends when both players pass on consecutive turns.  A player’s score is the sum of the sizes of all the trees which he owns.  The player with the higher score wins.